Understanding Levenshtein Transformer
Leveraging complementary yet adversarial techniques for sequence generation
1. Introduction
Neural sequence generation models are mostly autoregressive. An autoregressive model predicts future behavior based on past behavior [1]. In the case of seq2seq problems, the next token is generated based on the previous outputs, which is incompatible with humans, where we revise generated text. A Non-Autoregressive architecture [2], on the other hand, produces the entire output sequence in parallel, which leads to lower latencies during inference. This feature has significant implications in commercial systems.
Levenshtein Transformer [3] is a partially autoregressive model that addresses the pre-existing architectures' lack of flexibility. Trained using imitation learning, it has two policies, Insertion and Deletion, executed alternately.
2. Related Work
2.1. Non-Autoregressive Transformers (NAT)
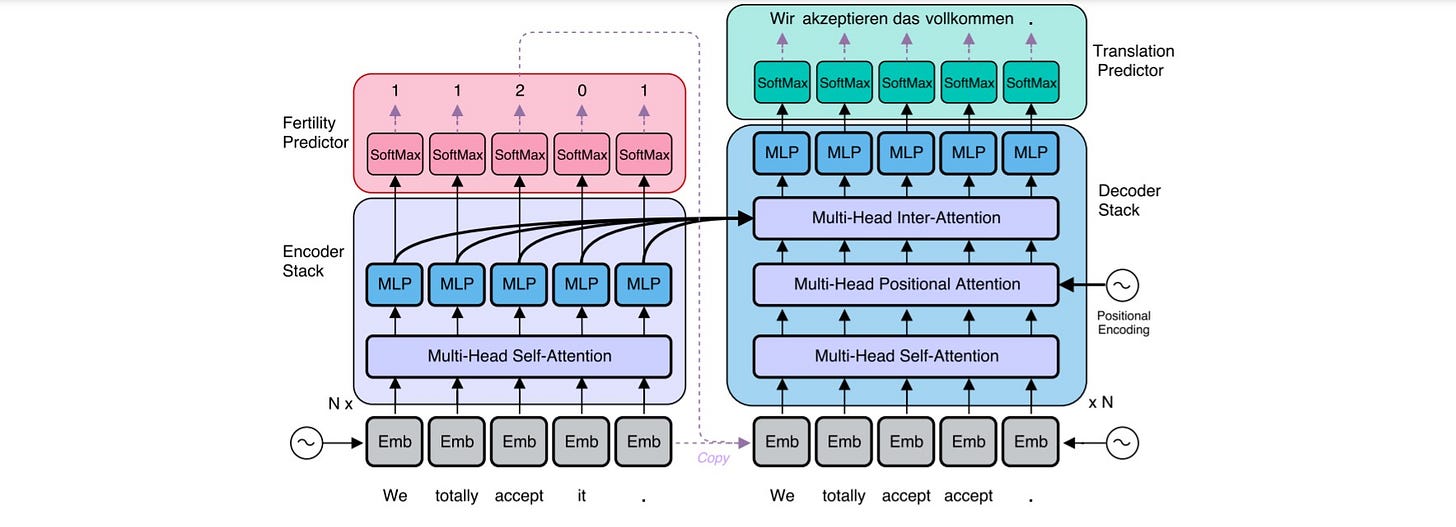
NAT [2] modifies the original Transformer network by adding a module that predicts fertilities, sequences of numbers that form an important component of many traditional MT models.
2.1.1. Encoder Stack
The encoder stays unchanged from the original Transformer network.
2.1.2. Decoder Stack
To translate non-autoregressively and parallelize the decoding process, the decoder is modified as follows.
2.1.2.1. Decoder Inputs
Before decoding, the architecture needs to know how long the target sentence will be to generate all words in parallel.
As the source and target sentences are often of different lengths, the authors propose two methods
Copying source inputs uniformly
Copying source inputs using fertilities
Copy each encoder input as a decoder input zero or more times, with the number of times each input is copied referred to as the input word's "fertility."
2.1.2.2. Non-causal self-attention
Since the output distribution will not be autoregressively factorized, the earlier decoding steps can now access information from later stages. To achieve this, each query position is masked from attending to itself.
2.1.2.3. Positional attention
An additional positional attention module is also included in each decoder layer, which is a multi-head attention module with the same general attention mechanism used in other parts of the Transformer network.
2.2. Markov Decision Process (MDP)
MDPs are an integral part of Reinforcement Learning and are used for modeling decision-making problems where the outcomes are partly random and partly controllable [4].
2.2.1. Markov Property
According to the Markov Property, the current state of an agent depends only on its immediate previous state (or the previous timestep).
2.2.2. Markov Process
A Markov Process is defined by (S, P) where S is the states, and P is the state-transition probability. It consists of a sequence of random states S1 → Sn where all the states obey the Markov property.
2.2.3. Markov Reward Process (MRP)
An MRP is defined by (S, P, R, γ), where S is the states, P is the state-transition probability, R_s is the reward, and γ is the discount factor.
2.2.4. Markov Decision Process (MDP)
An MDP is defined by (S, A, P, R, γ), where A is the set of actions. It is essentially MRP with actions.
3. Problem Formulation
3.1. Sequence Generation and Refinement
The authors' cast sequence generation and refinement to a Markov Decision Process (MDP). This setup consists of interacting with an environment that receives the agent's editing actions and returns a modified sequence. The reward function R measures the distance between the generated and the ground-truth sequence.
3.1.1. Actions: Deletion and Insertion
3.1.1.1. Deletion
The deletion policy reads the input sequence y, and for every token yi ∈ y, the deletion policy π del(d|i, y) makes a binary decision which is 1 (delete this token) or 0 (keep it).
3.1.1.2. Insertion
This involves two phases: placeholder prediction and token prediction so that it can insert multiple tokens at the same slot. First, among all the possible inserted slots, the insertion function predicts the possibility of adding one or several placeholders. The token prediction policy replaces the placeholders with actual tokens in the vocabulary.
3.1.1.3. Policy Combination
These complementary operations are now combined alternately. In sequence generation from the empty, insertion policy is first called followed by Deletion, repeated till the stopping condition is fulfilled.
One iteration of the sequence has three phases
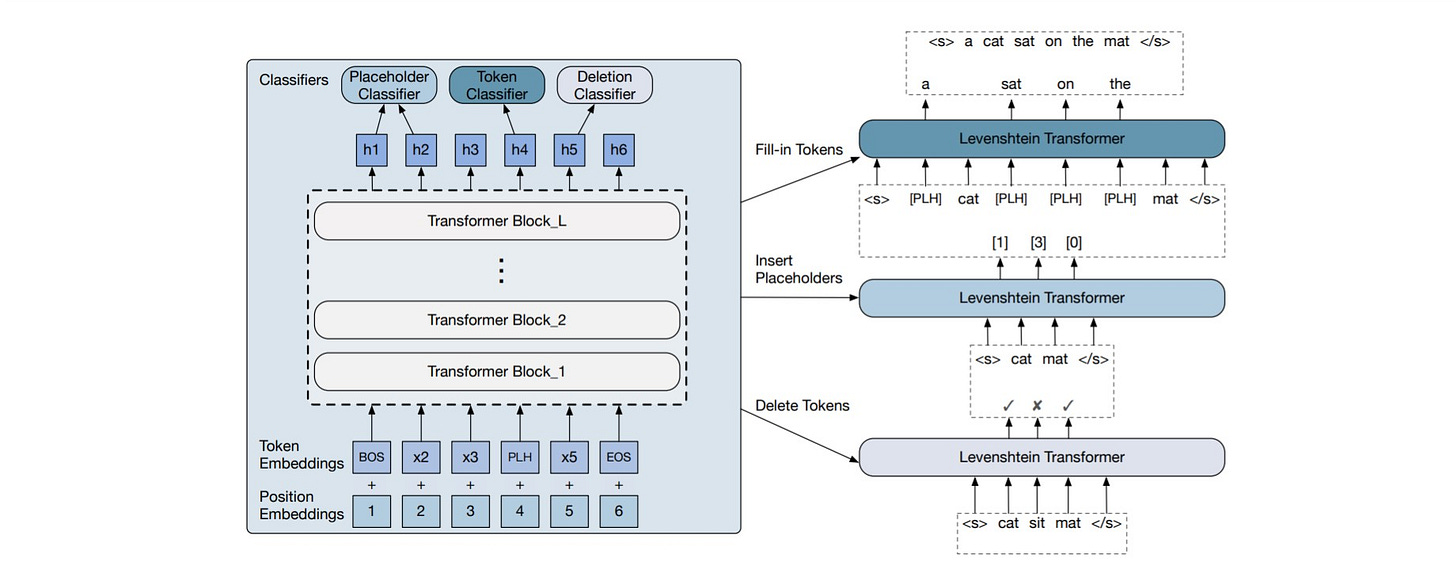
Delete tokens
Insert placeholders
Replace placeholders with new tokens
4. Levenshtein Transformer
4.1. Model
It uses Transformer as the basic building block.
4.1.1. Policy Classifiers
The decoder outputs are passed to three policy classifiers.
4.1.1.1 Deletion Classifier
The LevT scans over the input tokens and predicts "deleted" (0) or "kept" (1).
4.1.1.2. Placeholder Classifier
The LevT predicts the number of tokens inserted at every consecutive position pair. The placeholder is represented by a special token <PLH>.
4.1.1.3. Token Classifier
The LevT fills in the tokens by replacing all placeholders.
4.2. Dual-policy Learning
Imitation Learning is used to train the model. The agent learns to imitate the behaviors drawn from some expert policy.
4.2.1. Expert Policy
It is crucial to construct an expert policy in imitation learning that cannot be too hard or weak to learn from. The authors considered two types of experts.
4.2.2.1. Oracle
Here, the oracle has access to the ground-truth sequence.
4.2.2.2 Distillation
Here, an autoregressive teacher model is trained using the same dataset and then replaced with the ground-truth sequence by the beam-search result of the teacher model.
5. Why the name “Levenshtein”?
The reward function measures the distance between generated and the ground-truth sequence using the Levenshtein Distance formula.
6. Conclusion
We understood the basics of Non-Autoregressive models and Markov Decision Processes. Later we saw how the authors of the paper cast the problem of sequence generation to a Markov Decision Process, and the different actions the agent can take, Deletion and Insertion, and how the training procedure combines both. Finally, we look into the three different classifiers in the architecture: Deletion, Placeholder, and Token classifiers.
References
[1] Autoregressive Model: Definition & The AR Process

Good